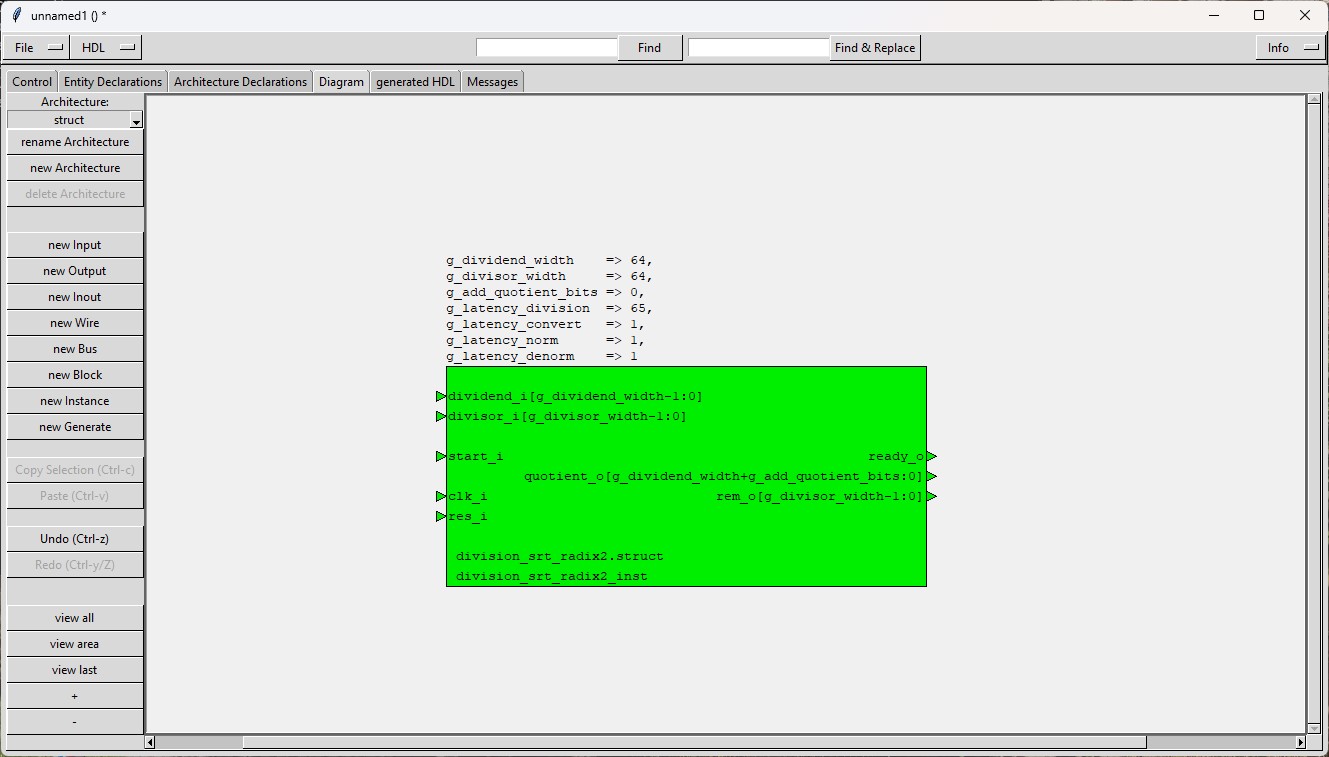
The module "division_srt_radix2"
a VHDL implementation of a radix2 SRT division algorithm on integer numbers

The module "division_srt_radix2" (see symbol) calculates the signed quotient and the signed remainder of an integer dividend and an integer divisor.
The calculation is performed without converting the dividend and the divisor into unsigned numbers.
But both operands are normalised prior to the start of the division operation.
So as the module "division", the module "division_srt_radix2" must complete an additional step before the division can be executed.
But in contrary to the "division" module no additional data bit is introduced by the normalization.

The "division" and the "division_signed" module determines a quotient bit by calculating all bits of an intermediate result.
The "division_srt_radix2" module, on the other hand, only calculates the 4 most significant bits of an intermediate result and
then "guesses" the quotient bit with the help of a small additional logic. Due to this additional logic, "division_srt_radix2" only
achieves better timing when the operands are wider than about 32 bits. This limit is of course technology-dependent and
must be determined experimentally.
The term "radix2" means that each quotient-bit must be multiplied with 2**-i (i= bitposition) to get
its contribution to the overall normalized quotient (there exist other SRT divisions with radix 4, 16, ...).

The number of bits of dividend and divisor are configured by generics.
Dividend, divisor, quotient and remainder are numbers in 2's complement format.
The quotient is first not calculated as a binary number but as a number with bit values +1, 0 or -1.
After the division the quotient is converted into a 2's complement number.
Both quotient and remainder are fixed in some cases.
The latency of the module can be configured by generics independently from the width of the operands.

This means, the module is configurable by generics in order

• to fulfill any requirements regarding the number of bits of the operands and
• to fulfill any requirements regarding its latency.

But of course there is no guarantee that timing closure can be reached with the selected values
for the generics, as the timing depends on the technology which is used at synthesis.

The module "division_srt_radix2" was developed with HDL-SCHEM-Editor.

Ports:

Port name	Direction	Description
res_i	input	asynchronous reset input, 1-active Can be clamped to 0 when all latency generics have the value 0.
clk_i	input	clock input Can be clamped to 0 when all latency generics have the value 0.
start_i	input	This input expects an 1-active impulse of 1 clock cycle width in order to start the calculation. When all latency generics have the value 0 then back to back pulses can be used.
dividend_i(g_dividend_width-1:0)	input	Signed dividend (g_dividend_width is a generic). The input is latched at start=1 when g_latency_norm is different from 0. Otherwise it must kept stable during the operation.
divisor_i(g_divisor_width-1:0)	input	Signed divisor (g_divisor_width is a generic). The input is latched at start=1 when g_latency_norm is different from 0. Otherwise it must kept stable during the operation.
ready_o	output	1-active impulse of 1 clock cycle width, when the calculation is ready (When all latency generics have the value 0 it gets active in the same clock cycle in which start_i gets active).
quotient_o(g_dividend_width+g_add_quotient_bits:0)	output	Signed quotient. Valid at ready_o=1 until the next start of a calculation or until the end of the next calculation if g_latency_convert or g_latency_denorm is different from 0.
rem_o(g_divisor_width-1:0)	output	Signed remainder. Valid at ready_o=1 until the next start of a calculation or until the end of the next calculation if g_latency_convert or g_latency_denorm is different from 0.

Generics:

Generic name	Minimum Value	Maximum Value	Description
g_dividend_width	5	none	Number of bits of the dividend The first bit represents the sign as the operands have to be coded in 2's complement.
g_divisor_width	3	none	Number of bits of the divisor The first bit represents the sign as the operands have to be coded in 2's complement.
g_add_quotient_bits	0	none	If this generic is different from 0, then additional quotient bits below the binary point for integer are calculated.
g_latency_norm	0	1	Latency (in clock cycles) of the sub-module division_srt_radix2_norm which normalizes dividend_i and divisor_i. When g_latency_norm is 0, then the sub-module is a combinatorial design. Bigger values than 1 are handled as 1.
g_latency_division	0	none	Latency of the division (in clock cycles) When g_latency_division is 0, then the division is implemented as a combinatorial design.
g_latency_convert	0	1	Latency (in clock cycles) of the sub-module division_srt_radix2_convert which converts quotient and remainder into binary format. When g_latency_convert is 0, then the sub-module is a combinatorial design. Bigger values than 1 are handled as 1.
g_latency_denorm	0	1	Latency (in clock cycles) of the sub-module division_srt_radix2_denorm and the sub-module division_srt_radix2_denorm_remainder which calculate the not normalized results. When g_latency_convert is 0, then the sub-module is a combinatorial design. Bigger values than 1 are handled as 1.

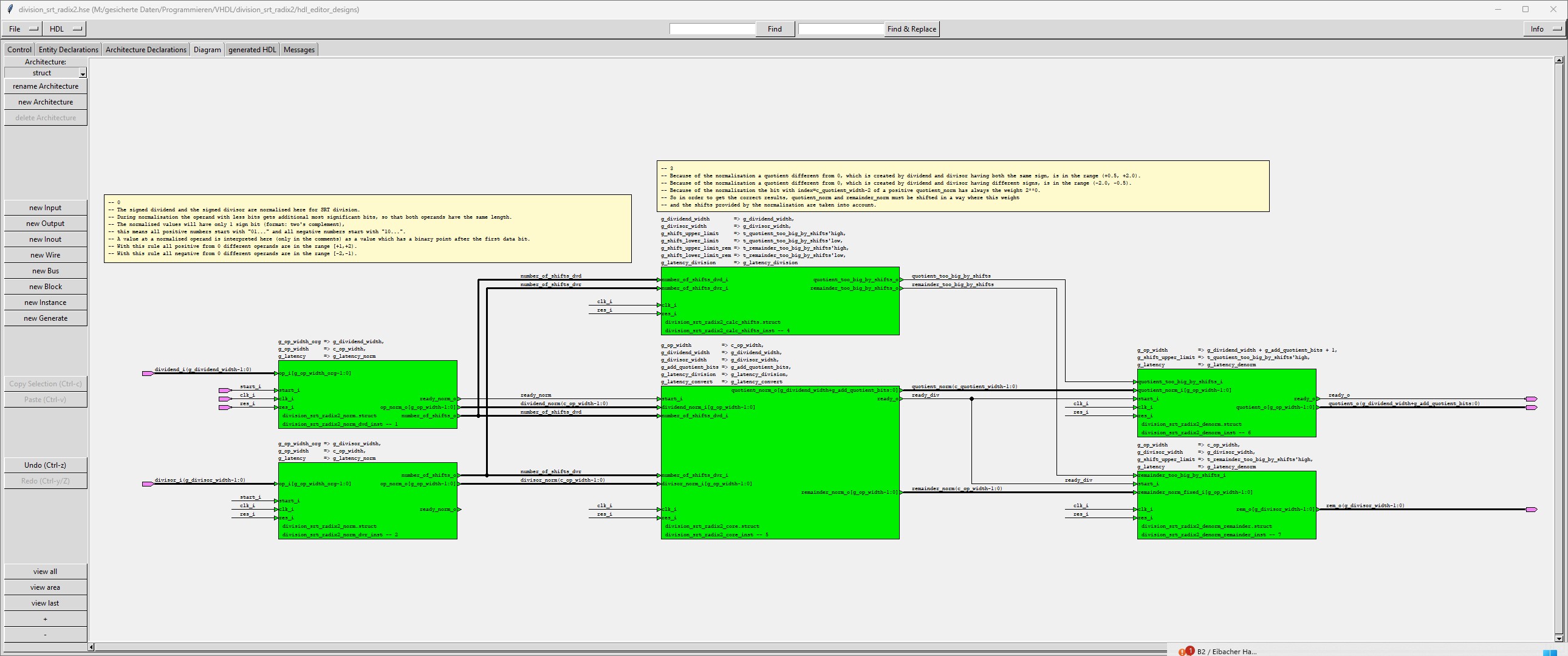
The module "division_srt_radix2" is a hierarchical module, which is built by these submodules:

Submodule name	Functionality
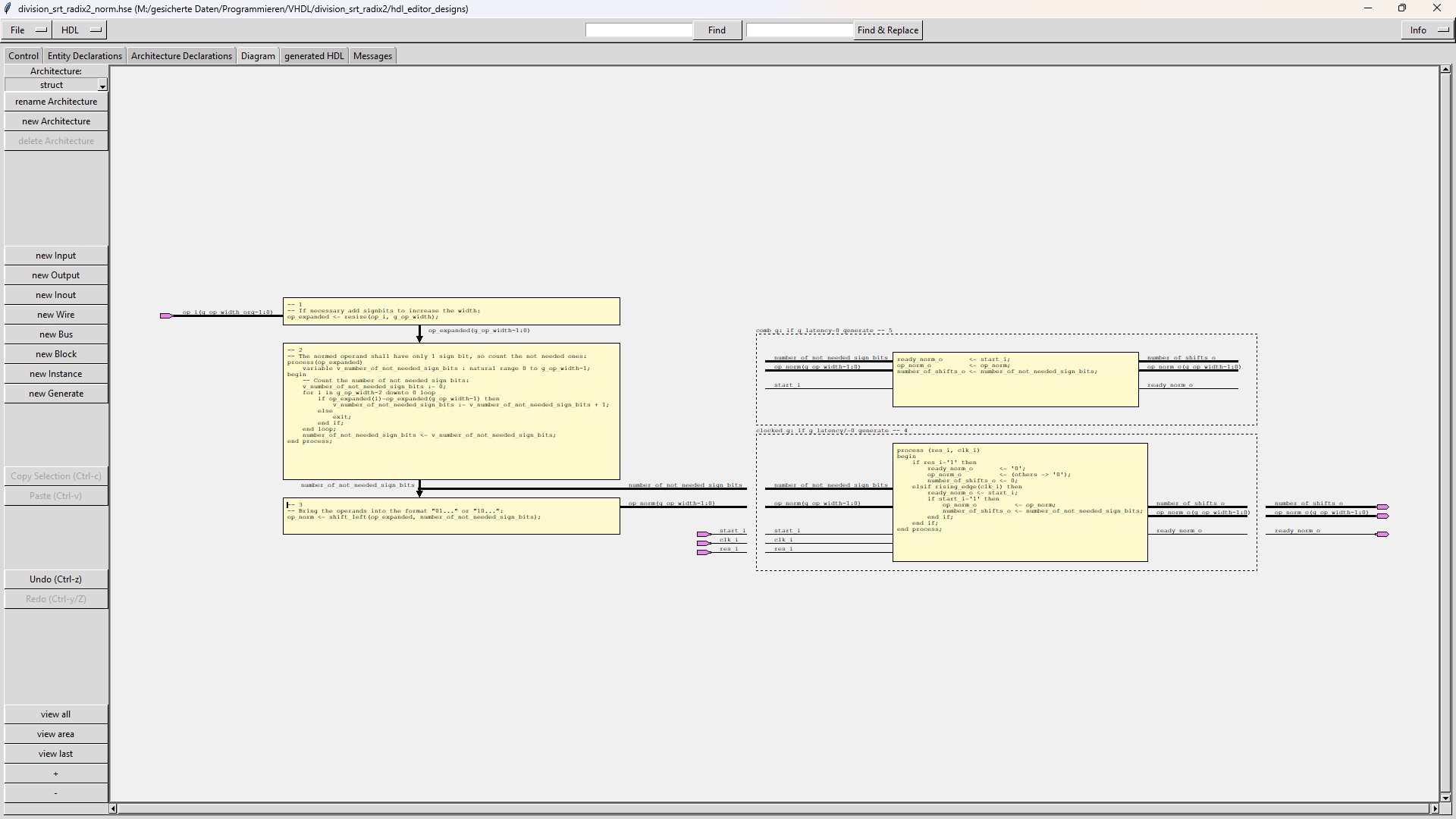
division_srt_radix2_norm	The sub-module "division_srt_radix2_norm" normalizes the dividend and the divisor. In a first step the sub-module resizes the operand from the original number of bits given by the generic g_op_width_org to the new operand width given by the generic g_op_width. This feature is used to increase the operand width of the smaller operand of dividend and divisor to the same size given by the bigger operand. In a second step the operand (always a 2's complement number) is shift left until the operand looks like "01..." or "10...". The number of executed shifts shows at the sub-module output "number_of_shifts_o". When the generic g_latency_norm is different from 0, then the shifted operand and the number of shifts are both stored in a register.
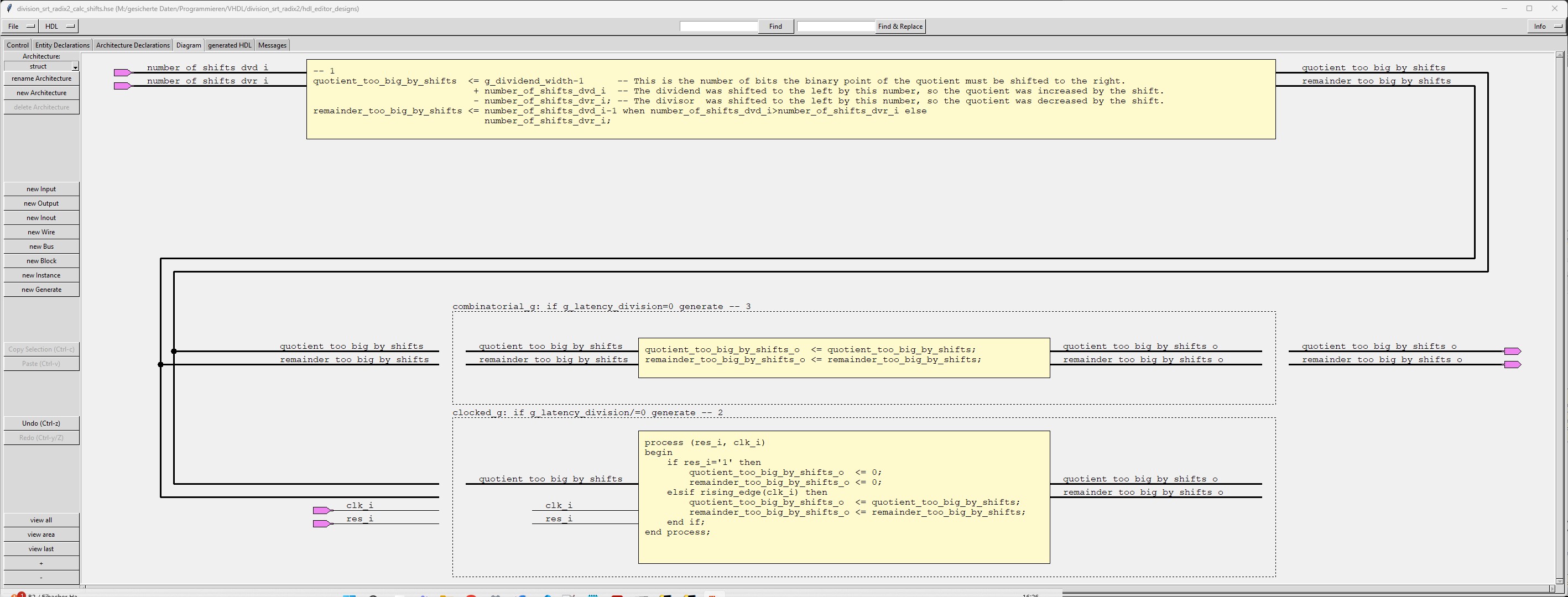
division_srt_radix2_calc_shifts	The sub-module "division_srt_radix2_calc_shifts" calculates the number of shifts for the de-normalization of quotient and remainder. When the generic g_latency_division is different from 0, then the calculated numbers are both stored in a register.
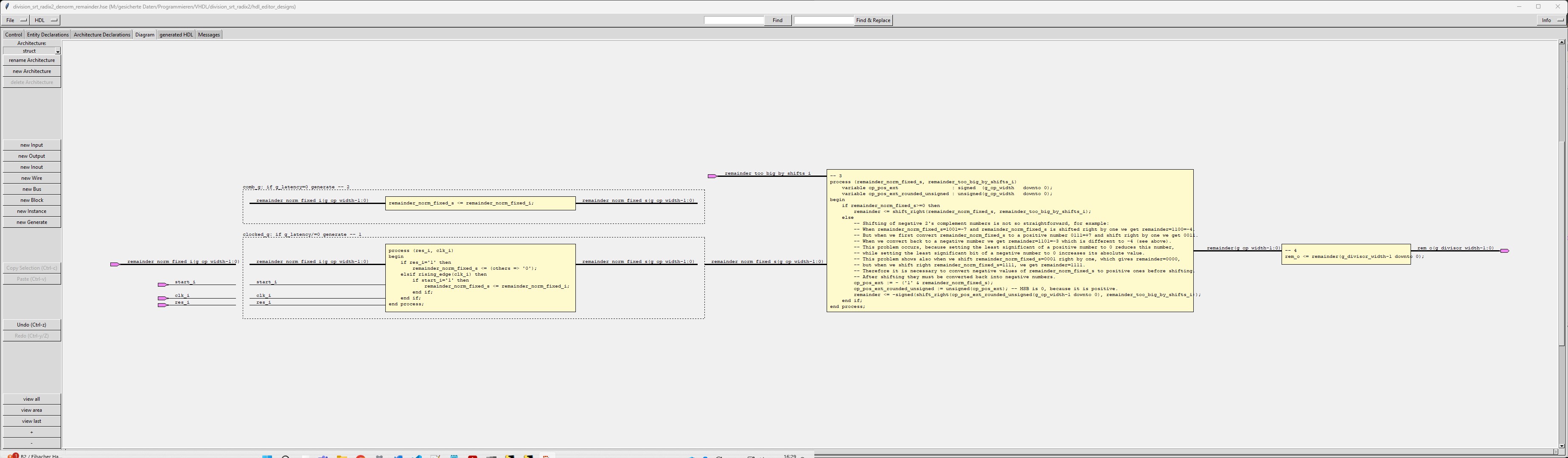
division_srt_radix2_denorm	The sub-module "division_srt_radix2_denorm" de-normalizes the quotient based on the shift-numbers calculated by "division_srt_radix2_calc_shifts" When the generic g_latency_denorm is different from 0, then the result is stored in a register.
division_srt_radix2_denorm_remainder	The sub-module "division_srt_radix2_denorm_remainder" de-normalizes the remainder based on the shift-numbers calculated by "division_srt_radix2_calc_shifts" When the generic g_latency_denorm is different from 0, then the result is stored in a register.
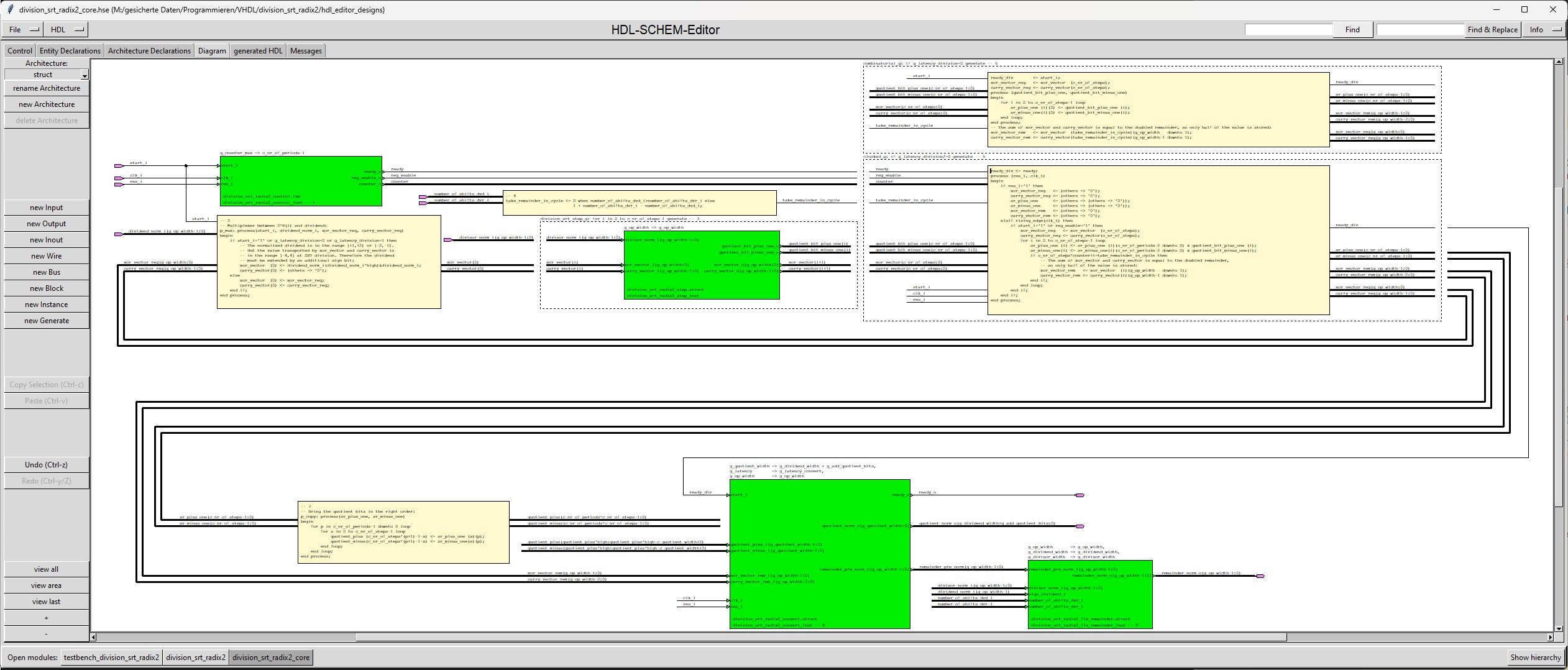
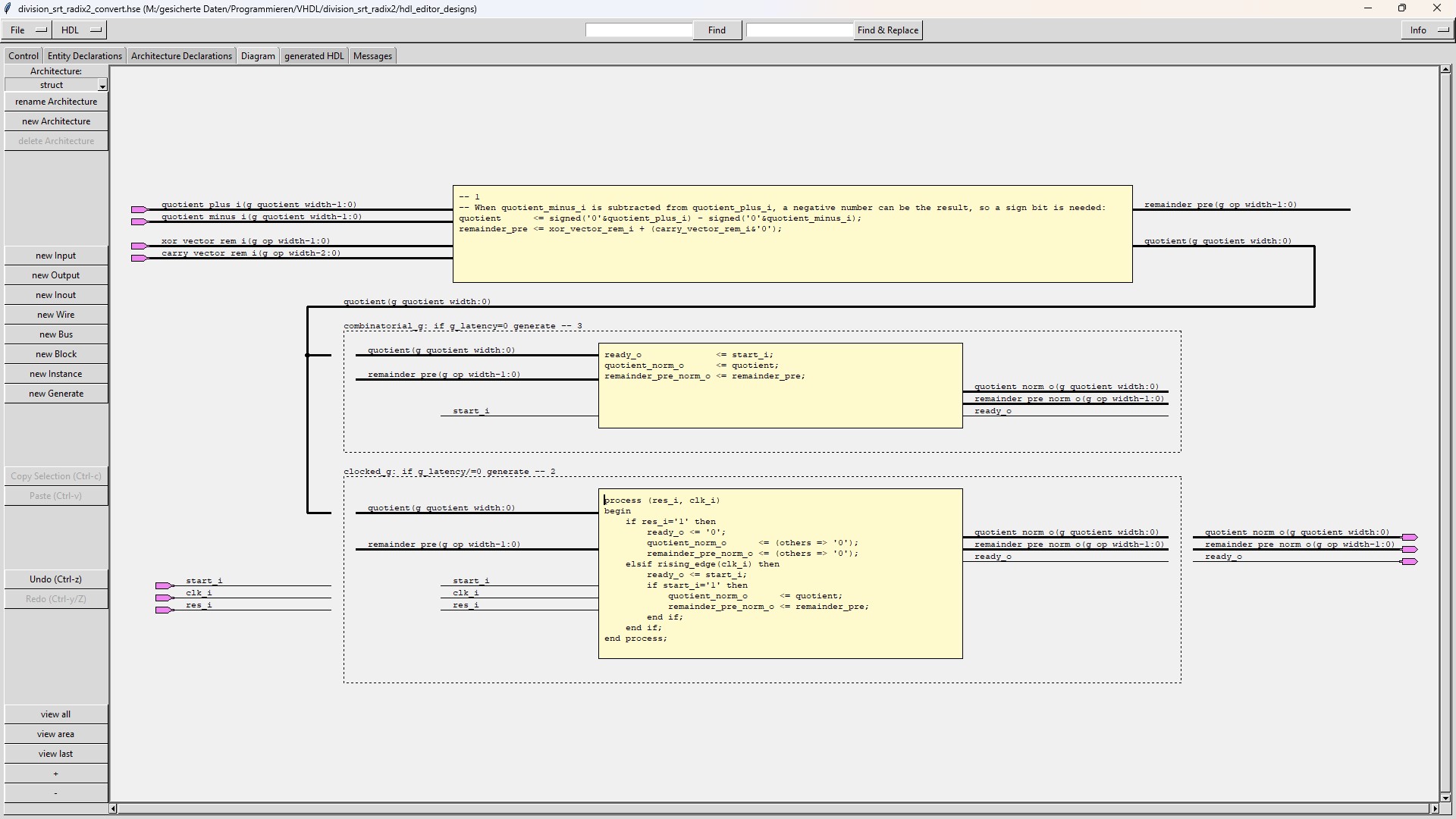
division_srt_radix2_core	The division_srt_radix2_core calculates the normalized quotient and the normalized remainder. The module can be used standalone if your system is based on normalized numbers. The inputs number_of_shifts_dvd_i and number_of_shifts_dvr_i must then be clamped to 0. The module "division_srt_radix2_core" uses the sub-module "division_srt_radix2_step" which performs 1 step of the algorithm and is instantiated several times depending on the generics g_dividend_width, g_add_quotient_bits and g_latency_division. The quotient bit which is calculated by "division_srt_radix2_step" is in a redundant number format and has one of the values -1, 0, +1. The sub-module "division_srt_radix2_step" is based on carry-save adders. The module "division_srt_radix2_core" uses the sub-module "division_srt_radix2_control" which enables registers and activates a ready signal when the division is done. The module "division_srt_radix2_core" uses the sub-module "division_srt_radix2_convert" which converts the redundant number format of the quotient into a 2's complement. It also calculates the remainder from the the carry-save-signals used by "division_srt_radix2_step". The module "division_srt_radix2_core" uses the sub-module "division_srt_radix2_fix_remainder" which fixes the remainder when it has the wrong sign or when it is equal to the negated divisor.
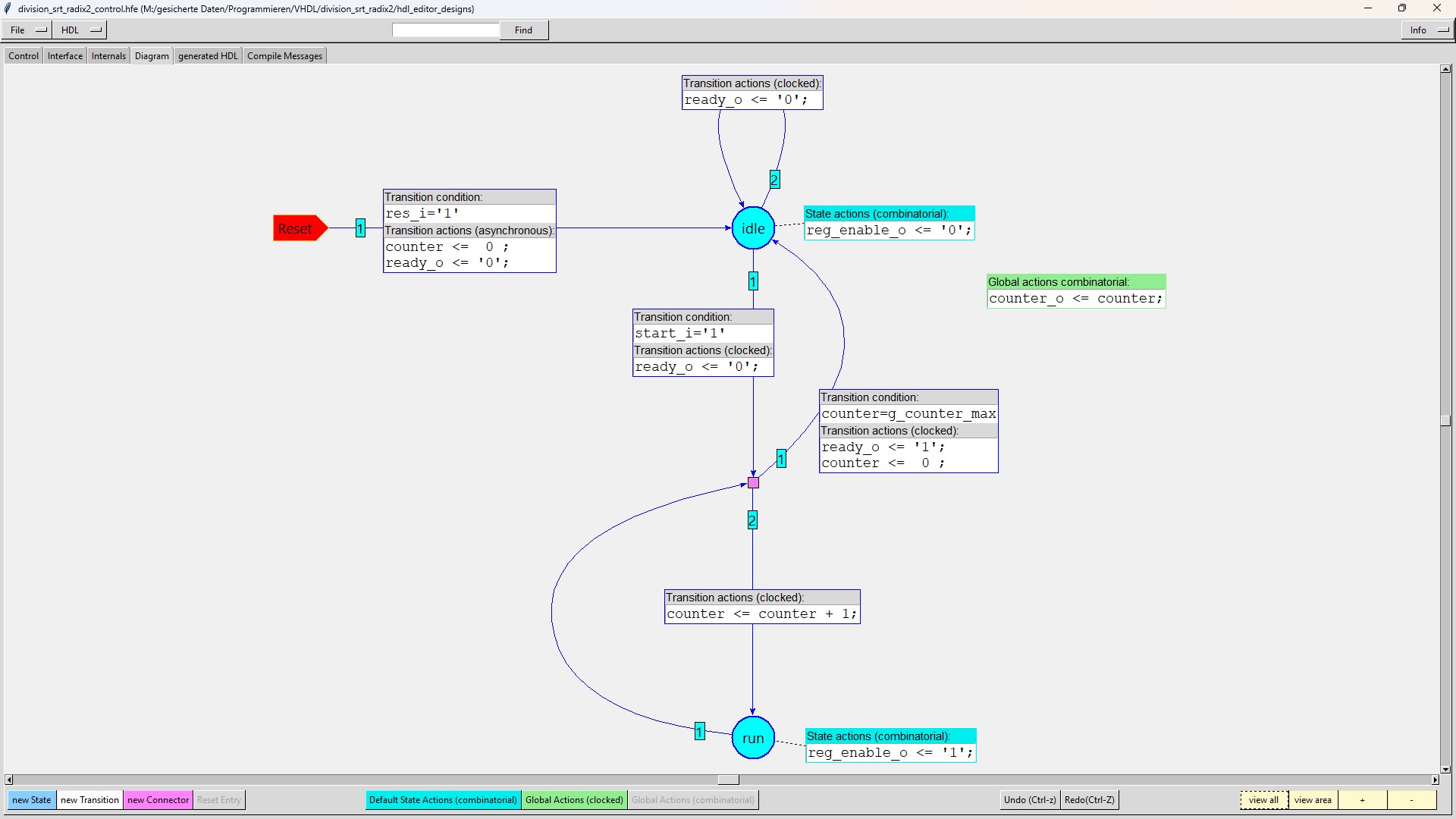
division_srt_radix2_control	The "division_srt_radix2_control" module enables the shift registers in which the quotient bits are stored (in redundant number format). The "division_srt_radix2_control" module enables the intermediate registers in which the carry-save signals from "division_srt_radix2_step" are stored. The "division_srt_radix2_control" module activates a ready signal for the division if g_latency_division is different from 0.
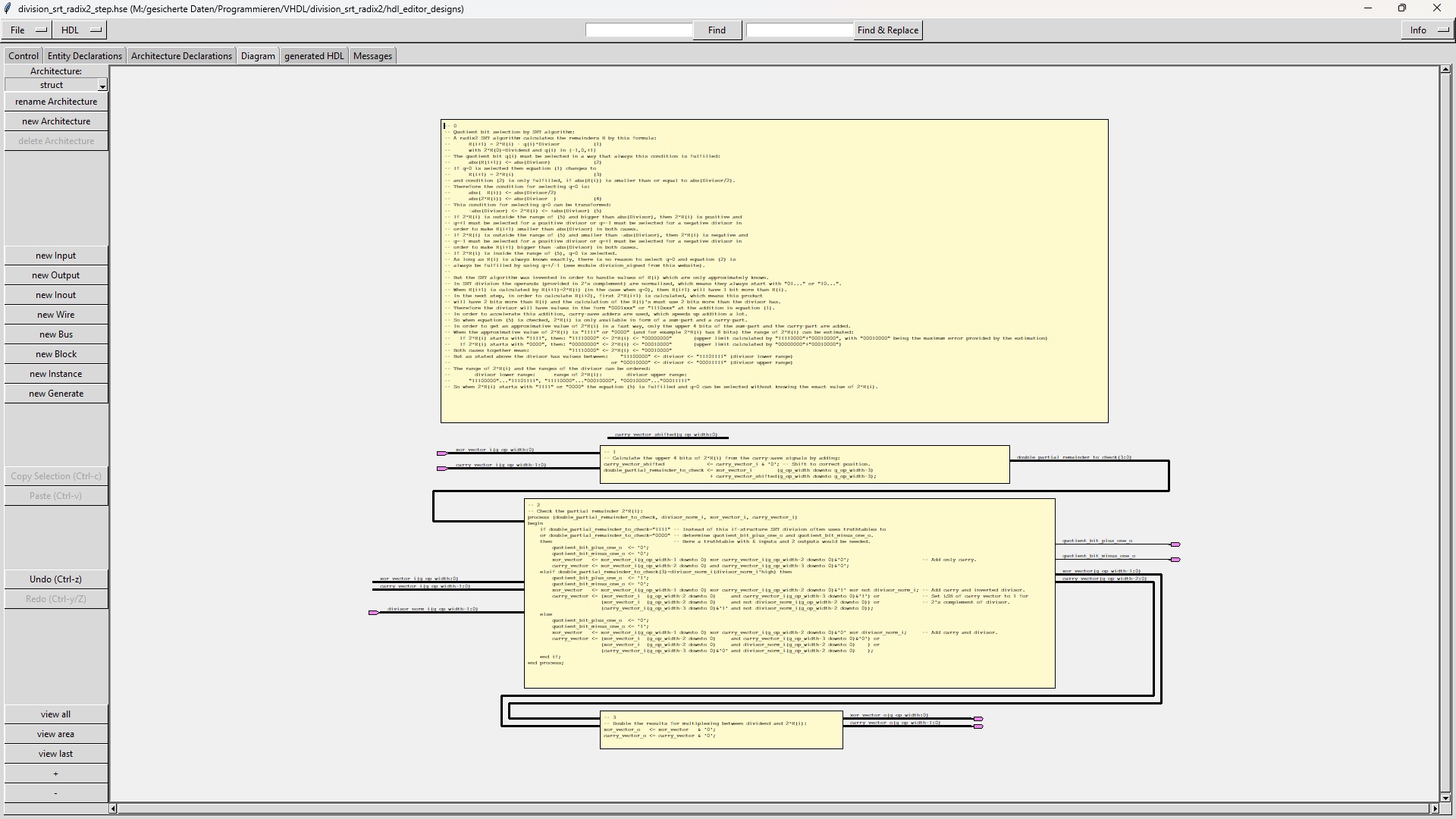
division_srt_radix2_step	The "division_srt_radix2_step" module calculates the 4 most significant bits of the intermediate result from the carry-save signals. Afterwards the module checks the 4 most significant bits of the intermediate result and sets the quotient bit to -1, 0 or +1. Depending at the calculated quotient bit the new carry-save signals are calculated.
division_srt_radix2_convert	The "division_srt_radix2_convert" module converts the quotient with bit-values -1, 0 or +1 into a 2's complement number. The "division_srt_radix2_convert" module calculates the remainder from the carry-save signals. If the generic g_latency_convert is different from 0, then the results are stored in a register.
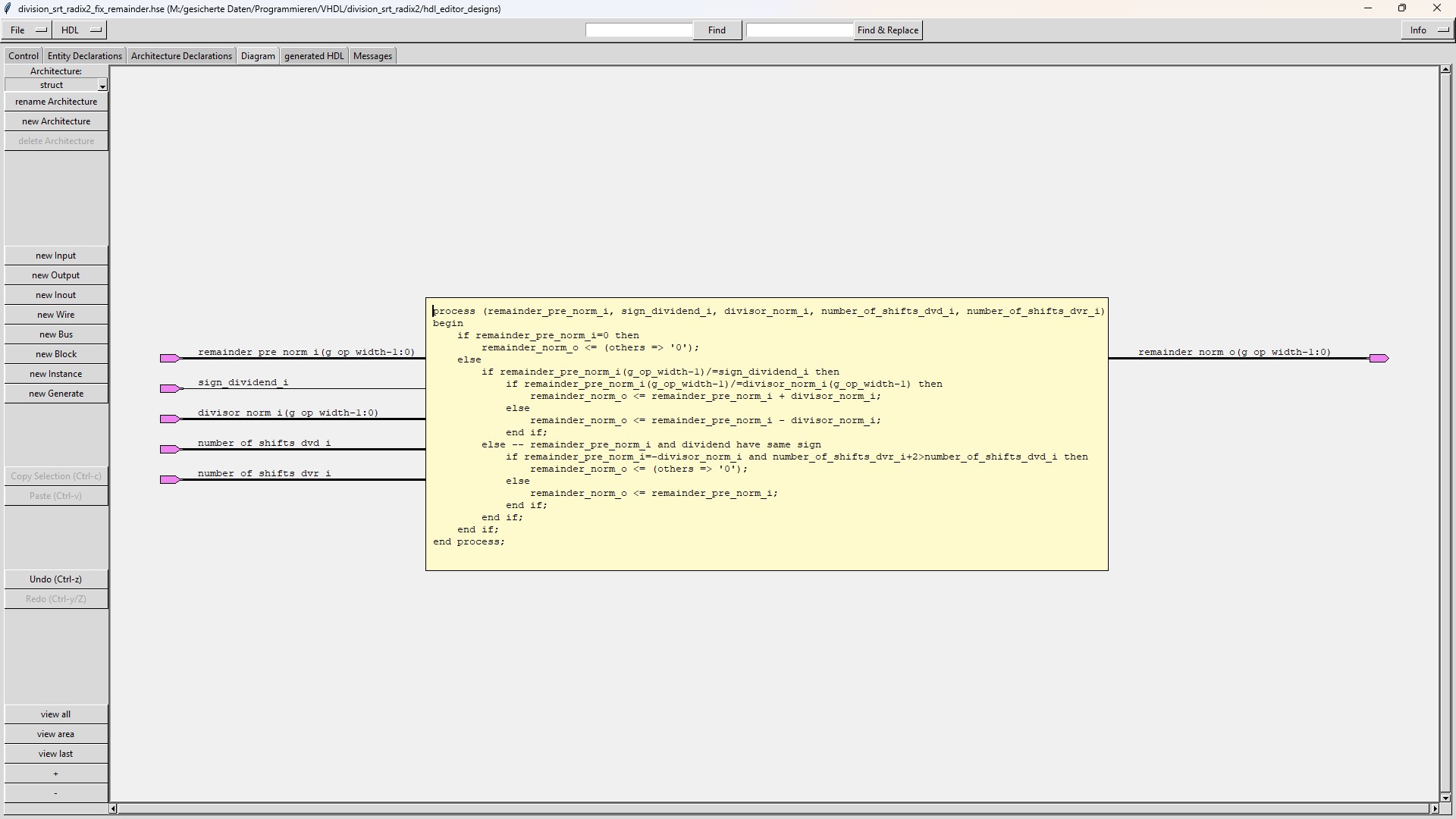
division_srt_radix2_fix_remainder	The sub-module "division_srt_radix2_fix_remainder" fixes the remainder when it has the wrong sign or when it is equal to the negated divisor. The sub-module "division_srt_radix2_fix_remainder" is a combinatorial module and does not have any register.

There are no limitations for the generics g_dividend_width and g_divisor_width (except that they cannot be smaller than their minimum value).
These generics are most of the time determined by the environment, where the module division_srt_radix2 is used.

When the generic g_add_quotient_bits is different from 0, more steps of the division algorithm have to be executed,
which causes more hardware effort and longer calculation time.

There is also no limitation for the generic g_latency_division, but the smaller the value is chosen,
the harder it will get to reach timing closure.

The optimal value for g_latency_division can be calculated in this way:
The number of quotient bits which are calculated is given by the sum g_dividend_width+1+g_add_quotient_bits (the
"+1" in this sum is caused by a division when the smallest negative number is divided by -1, because then
an additional bit is needed to present the quotient in 2's complement).
So when g_latency_division=g_dividend_width+1+g_add_quotient_bits then 1 bit of of the quotient is calculated
in 1 clock cycle, which is the optimal value for reaching time closure.

If g_latency_division is bigger than g_dividend_width+1+g_add_quotient_bits, then also 1 bit of the quotient is
calculated in each clock cycle, but the additional quotient bits are not connected to the output.

If g_latency_division is smaller than g_dividend_width+1+g_add_quotient_bits, then more than 1 bit of the quotient
must be calculated in 1 clock cycle. This makes reaching timing closure more difficult.

Setting g_latency_norm different from 0, increases the overall latency by 1 clock cycle but makes reaching timing closure easier.

Setting g_latency_convert different from 0, increases the overall latency by 1 clock cycle but makes reaching timing closure easier.

Setting g_latency_denorm different from 0, increases the overall latency by 1 clock cycle but makes reaching timing closure easier.

Source code for HDL-SCHEM-Editor and HDL-FSM-Editor of the VHDL-module "division_srt_radix2" and its testbench (Number of downloads = 25 ).
With these files the schematics and the state-diagram of module division_srt_radix2 can be loaded into HDL-SCHEM-Editor or HDL-FSM-Editor and can easily be read and modified:

• hdl_editor_designs.zip

All module VHDL-files of the module "division_srt_radix2" (Number of downloads = 39 ).
These files were generated by HDL-SCHEM-Editor and HDL-FSM-Editor:

• VHDL_designs.zip

All testbench VHDL-files of the testbench of the module "division_srt_radix2" (Number of downloads = 33 ).
These files were generated by HDL-SCHEM-Editor and HDL-FSM-Editor:

• VHDL_testbenches.zip

Relocation hints:

You should extract all archives into a folder named "division_srt_radix2".
Then you must replace "M:/gesicherte Daten/Programmieren/VHDL/division_srt_radix2" in all "hdl_editor_designs/*.hse" source files by your path to this directory.
Now you can navigate through the design by HDL-SCHEM-Editor and generate HDL by HDL-SCHEM-Editor for all modules except division_srt_radix2_control,
for which the HDL must be generated by HDL-FSM-Editor.
Of course there is only need for generating HDL, if you change something at the modules, because you can find the HDL in VHDL_designs.zip and VHDL_testbenches.zip.
If you want to simulate or modify the modules by HDL-SCHEM-Editor you also must adapt the information in the Control-tab of the toplevel you want to work on.
There you must define a "Compile through hierarchy command", an "Edit command", the path to your HDL-FSM-Editor and a "Working directory".

Change log:

Version 1.0 (11.09.2024):

• Initial version

Version 1.1 (29.09.2024):

• An alternative architecture "pla" for the module division_srt_radix2_step was added.
  In this architecture a table is used for determining the quotient bits.

If you detect any bugs or have any questions,
please send a mail to "matthias.schweikart@gmx.de".